A majority of the drone related applications are outdoors and potentially involve environments with large wing gusts. Large wind gusts have the potential to destabilize the quadrotor if the flight controller is not equipped to cope with these disturbances.
In this project we will design a transfer function to help restabalize a drone after a gust of wind. We will also design a similar system controlled by an AI algorithm and compare the results of the experiments.
For machines to successfully operate in the real world and interact with their environment, they need to be able to learn throughout their deployment, acquire new skills without compromising old ones, adapt to changes, and apply previously learned knowledge to new tasks - all while conserving limited resources such as computing power, memory and energy. These capabilities are collectively known as Dynamic Adaptation. We take inspiration from biological processes and neural architectures and develop algorithms to overcome these challenges.
My research focuses on both development of algorithms as well as supporting hardware architectures to facilitate lifelong learning. Today we will compare control systems developed using traditional methods to those controlled by neural networks and genetic algorithms.
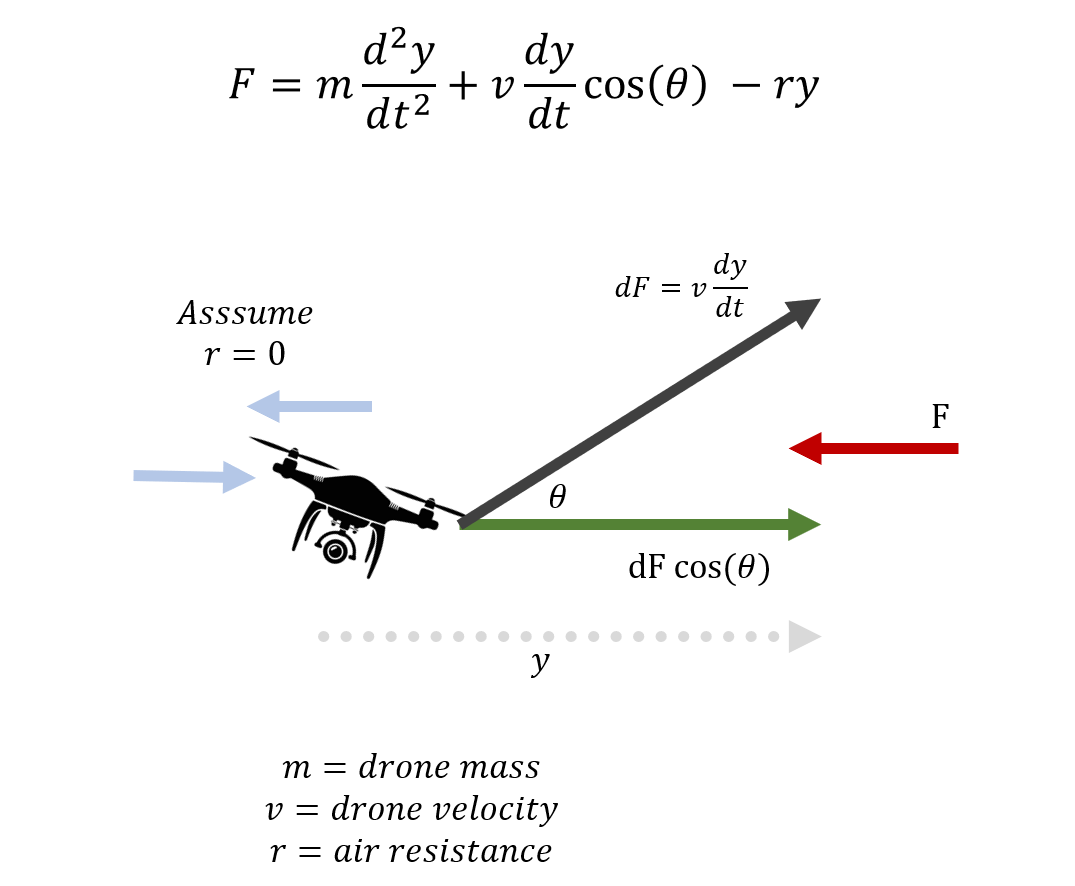
We first identify our input and output spaces, and the corresponding variables. We denote the wind as force F, and hence model the equation for force counterbalance as shown.
V and Theta are control variables assigned to the drone. They are modelled to respond programmatically and control the quadcopter motors to create the resultant velocity (V) and angular tilt (Theta) as required.
The air resistance (r) is assumed to be zero. This is an oversimplification, but modelling air resitance dynamics is beyond the project scope. Additionally, as the air resistance will oppose drone moment along y when wind is applied, as well as opposite y when the drone is propelled to compensate. We can assume the dynamics to be accounted for, if not minimized by this phenomenon, in this particular case.
Using this equation we can use the laplace transform (LT) to derive the transfer function (TF).
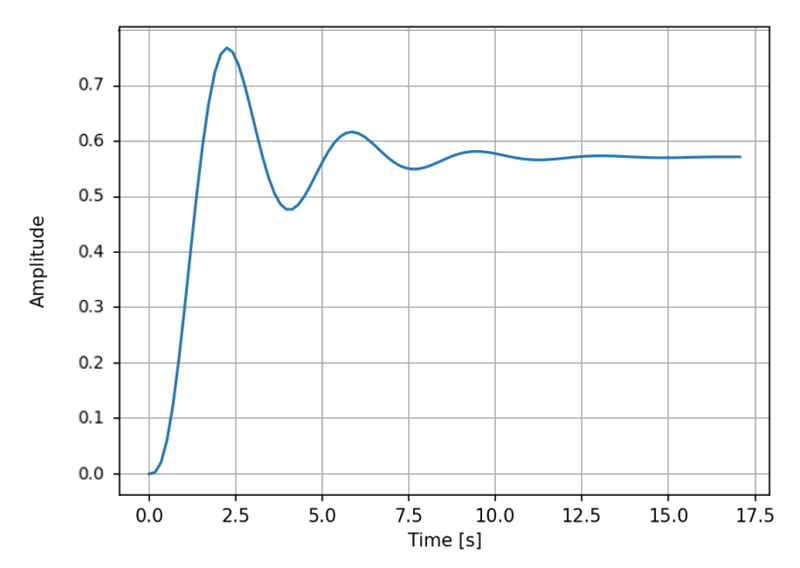
After obtaining the baseline transfer function which fits to the system given ranges of velocity and theta (max), we observe that the baseline transfer function takes ~12 seconds to stabilize. It suffers from overcorrection and large oscillations due to unrefined TF.
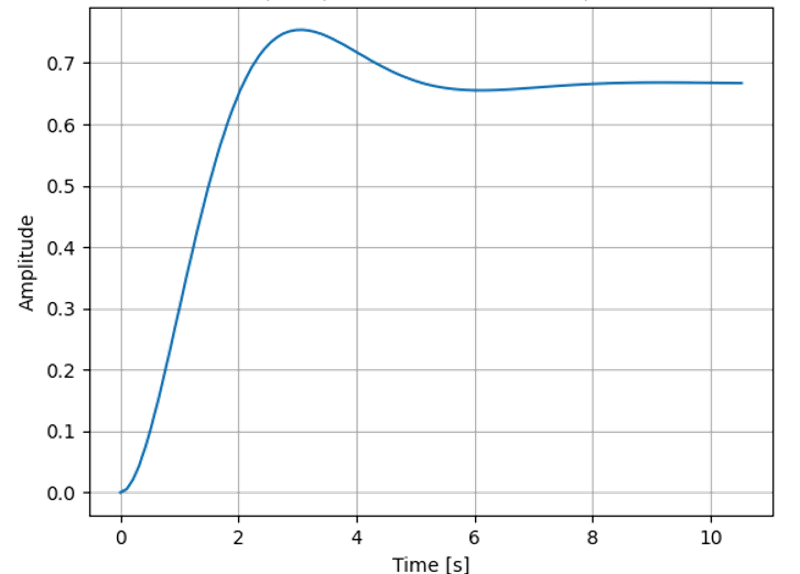
Using a Monte Carlo search for the TF parameters for faster stability, we are able to reduce the stabilization time to ~7 seconds. Although, it still has overcorrection, the oscillations are greatly reduced.
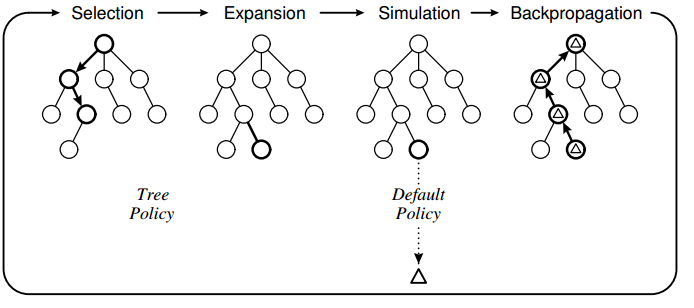
Monte Carlo Tree Search is a search technique in the field of Artificial Intelligence (AI). It is a probabilistic and heuristic driven search algorithm that combines the classic tree search implementations alongside machine learning principles of reinforcement learning. In tree search, there's always the possibility that the current best action is actually not the most optimal action. In such cases, MCTS algorithm becomes useful as it continues to evaluate other alternatives periodically during the learning phase by executing them, instead of the current perceived optimal strategy. This is known as the exploration-exploitation trade-off.
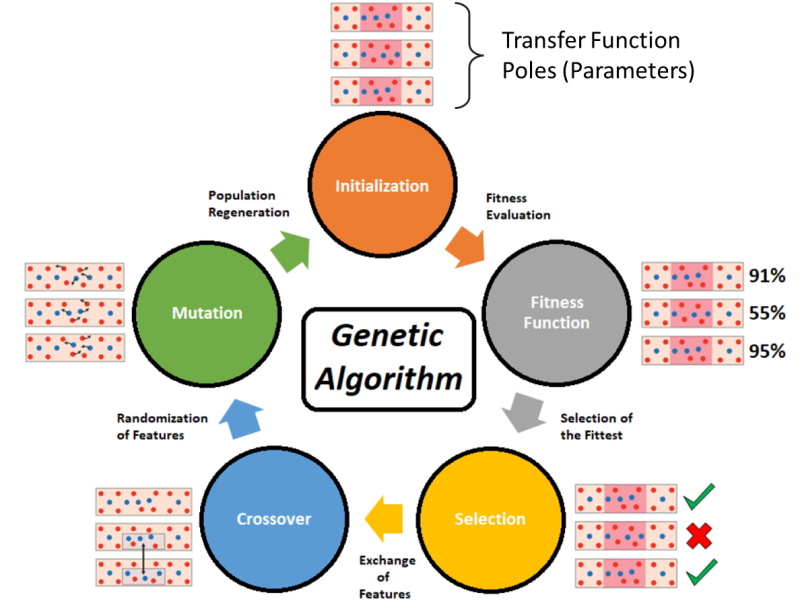
In a genetic algorithm, a population of candidate solutions to the transfer function are evolved toward better solutions. A genetic algorithm produces generations of possible parameters to satisfy the function.
The fitness function is evaluated for all produced variants in a generation. The most fit pairs (~top 10%) are selected to produce the next generation of parameters.
This process involves crossover and mutation. Crossover is the process by which parameters are exchanged between the best performing members and Mutation is the process by which member parameters are randomly perturbed to introduce variations and explore the solution space beyond the scope of the existing generation.
Can the genetic algorithm find better solutions than the monte carlo search, given time constraints of 15 minutes ?
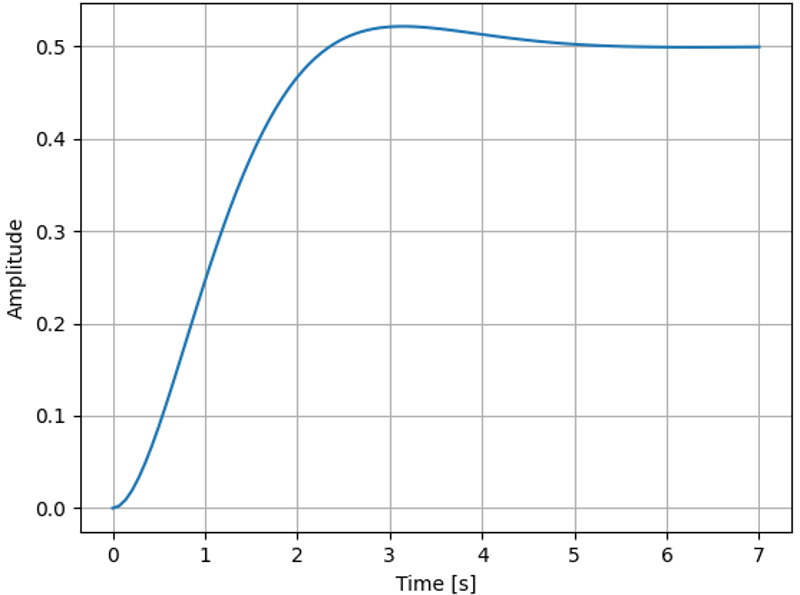
Using a Genetic Algorithm Optimizer for the TF parameters, we are able to reduce the stabilization time to ~5 seconds. There is minimal overcorrection. However, the Genetic Algorithm required much larger memory for computing every population.

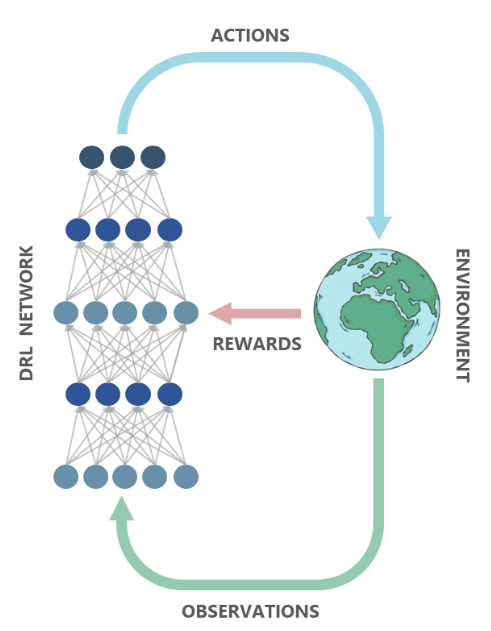
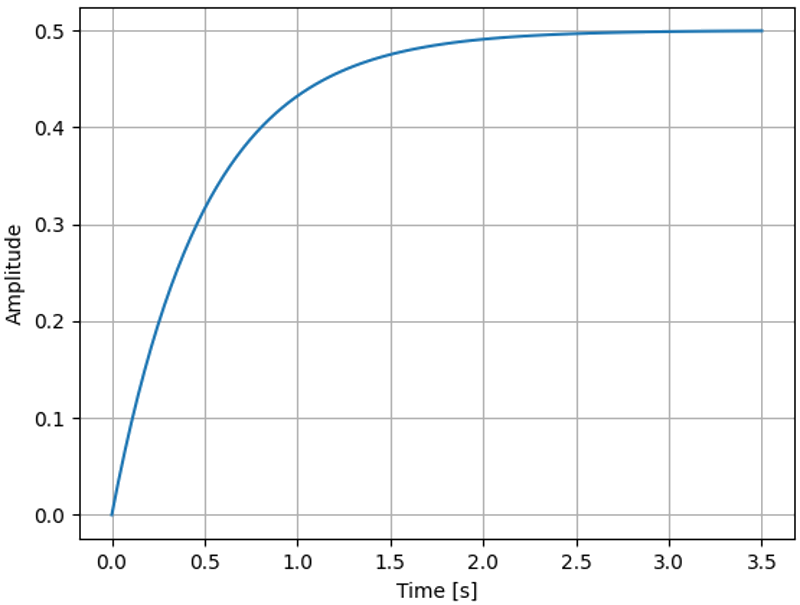
Reinforcement Learning does not operate on the TF parameters, instead it directly models the input gyro sensor to output motor control relationships. we are able to reduce the stabilization time to ~2.5 seconds. The overcorrection is almost completely rectified.




We observe that reinforcement learning approaches are free of traditional optimization constraints, and are able to explore a larger solution space than genetic algorithms and monte-carlo searches. However, training RL models requires considerably larger compute overheads as compared to these methods, while having a smaller memory footprint. Manual pole placement can be exaughstive and results in less than optimal solutions for more complex porblems.
This guy received his Bachelors in Electrical enginering form VIT, India and a Masters in Computer Engineering from Rochester Institute of Technology in 2019. He is curently pursuing his PhD in Electrical Engineering at the University of Texas at San Antonio. His research covers analysis and development of algorithms for adapting RL agents to dynamic environments and continual learning.